6.4. Introdução à Analise de Séries Temporais
6.4.2. |
O que são as Técnicas de Suavização ou Média Móvel? |
There are two distinct groups of smoothing methods
- Métodos de Cálculo da Média
- Métodos de Suavização Exponencial
O gerente de um depósito quer saber quanto um fornecedor típico entrega em unidades de 1000 dólares. Ele/ela tomam uma amostra dos 12 fornecedores, aleatórios, obtendo os seguintes resultados:
| Fornecedor | Quantia | Forneecedor | Quantia |
|---|---|---|---|
|
|
|||
| 1 | 9 | 7 | 11 |
| 2 | 8 | 8 | 7 |
| 3 | 9 | 9 | 13 |
| 4 | 12 | 10 | 9 |
| 5 | 9 | 11 | 11 |
| 6 | 12 | 12 | 10 |
Esta é uma estimativa boa ou ruim?
- O "erro" = quantia verdadeira gasta menos a quantia estimada.
- O "erro quadrático" é o erro acima, ao quadrado.
- O "SSE" é a soma dos erros quadráticos.
- O "MSE" é a média dos erros quadráticos.
A estimativa = 10
| Fornecedor | $ | Erro | Erro Quadrático |
|---|---|---|---|
|
|
|||
| 1 | 9 | -1 | 1 |
| 2 | 8 | -2 | 4 |
| 3 | 9 | -1 | 1 |
| 4 | 12 | 2 | 4 |
| 5 | 9 | -1 | 1 |
| 6 | 12 | 2 | 4 |
| 7 | 11 | 1 | 1 |
| 8 | 7 | -3 | 9 |
| 9 | 13 | 3 | 9 |
| 10 | 9 | -1 | 1 |
| 11 | 11 | 1 | 1 |
| 12 | 10 | 0 | 0 |
Realizando os mesmos cálculos chegamos em:
| Estimator | 7 | 9 | 10 | 12 |
|---|---|---|---|---|
|
|
||||
| SSE | 144 | 48 | 36 | 84 |
| MSE | 12 | 4 | 3 | 7 |
O estimador com menor MSE é o melhor. Pode ser mostrado matemáticamaente que o estimador que minimiza o MSE para um conjunto de dados aleatórios é a média.
A próxima tabela dá o lucro antes dos impostos de um fabricante de PC entre 1985 e 1994.
| Ano | $ (milhões) | Média | Erro | Erro Quadrático |
|---|---|---|---|---|
|
|
||||
| 1985 | 46.163 | 48.776 | -2.613 | 6.828 |
| 1986 | 46.998 | 48.776 | -1.778 | 3.161 |
| 1987 | 47.816 | 48.776 | -0.960 | 0.922 |
| 1988 | 48.311 | 48.776 | -0.465 | 0.216 |
| 1989 | 48.758 | 48.776 | -0.018 | 0.000 |
| 1990 | 49.164 | 48.776 | 0.388 | 0.151 |
| 1991 | 49.548 | 48.776 | 0.772 | 0.596 |
| 1992 | 48.915 | 48.776 | 1.139 | 1.297 |
| 1993 | 50.315 | 48.776 | 1.539 | 2.369 |
| 1994 | 50.768 | 48.776 | 1.992 | 3.968 |
O MSE = 1.9508.
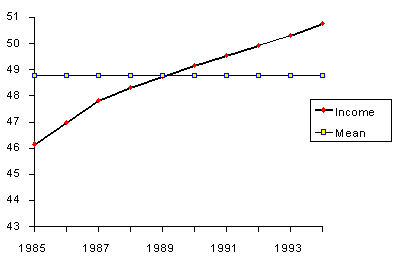
- A média "simples" de todas as observações passadas é somente uma estimativa para previsão quando não houver tendências. Se existirem tendências, use estimativas diferentes daquelas que levam a tendência em consideração.
- A média "pondera" todas as observações passadas igualmente. Por exemplo, a média dos valores 3, 4, 5 é 4. Sabemos, é claro, que uma média é calculada adicionando todos os valores e dividindo a soma pelo número de valores. outra maneira de se calcular a média é adicionando cada valor dividido pelo número de valores, ou
-
3/3 + 4/3 + 5/3 = 1 + 1.3333 + 1.6667 = 4.
O multiplicador 1/3 é chamado de peso. Em geral:
![xbar = (1/n)*SUM[i=1 to n]x(i) =
(1/n)*x1 + (1/n)*x2 + ... + (1/n)*Xn](eqns/xwmean.gif)
Os
 são os pesos e é claro eles devem somar 1.
são os pesos e é claro eles devem somar 1.

