6.4. Introdução à Analise de Séries Temporais
6.4.4. Modelos Univariados de Séries Temporais
6.4.4.4. |
Abordagens Comuns para Séries Temporais Univariadas |
Suavização exponencial tripla é um exemplo desta abordagem. Outro exemplo, chamado loess (sedimento eólico) sazonal, é baseado nos mínimos quadrados ponderados localmente e é discutido por Cleveland (1993). Não discutiremos loess sazonais neste manual.
Discussões detalhadas dos métodos baseados em frequências estão incluídas no Bloomfield (1976), Jenkins e Watts (1968), e Chatfield (1996).
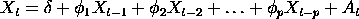
![delta = (1 - SUM[i=1 to p][phi(i)])*mu](eqns/armean.gif)
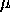 denotando a média do processo.
denotando a média do processo.
Um modelo autoregressivo é simplesmente uma regressão linear dos valores atuais da série contra um ou mais valores da série. O valor de p é chamado ordem do modelo AR.
Os modelos AR podem ser analisados com um dos vários métodos, incluindo técnicas dos mínimos quadrados lineares padrões. Eles também têm uma interpretação simples.
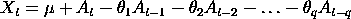
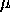 é a média da série, At-i são os ruídos brancos, e
é a média da série, At-i são os ruídos brancos, e
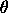 1,
... ,
1,
... ,
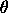 q
são os parâmetros do modelo.
O valor de q é chamado de ordem do modelo MA.
q
são os parâmetros do modelo.
O valor de q é chamado de ordem do modelo MA.
Isto é, um modelo de média móvel é conceitualmente uma regressão linear do valor corrente da série contra o ruído branco ou choques aleatórios de um ou mais valores anteriores da série. Os choques aleatórios em cada ponto são assumidos ser da mesma distribuição, geralmente uma distribuição normal, com localização em zero e escala constante. A distinção neste modelo é que estes choques aleatórios são propagados aos valores futuros da série temporal. Ajustar as estimativas MA é mais complicado do que com modelos AR devido aos erros não observáveis. Isto significa que procedimentos de ajuste não lineares iterativos precisam ser usados no lugar dos mínimos quadrados lineares. Os modelos MA também têm uma interpretação menos óbvia que os modelos AR.
Algumas vezes o ACF e PACF sugerirão que um modelo MA seria o modelo de melhor escolha e algumas vezes ambos os termos AR e MA deverão ser usados no mesmo modelo (ver Seção 6.4.4.5).
Note, entretanto, que os termos de erro após o modelo ser ajustado deverão ser independentes e seguirem as hipótese padrões para um processo inivariado.
Embora ambas as abordagens autoregressivas e de média móvel fossem já conhecidas (e foram investigadas originalmente por Yule), a contribuição de Box e Jenkins foi no desenvolvimento de uma metodologia sistemática para identificar e estimar modelos que pudessem incorporar ambas as abordagens. Isto torna os modelos Bx-Jenkins uma poderosa classe de modelos. As várias próximas seções discutirão estes modelos em detalhes.

